0. 그래프
그래프는 아이템과 이들 사이의 연결 관계를 표현하는 자료구조이다.
그래프는 정점(Vertex)들의 집합과 이들을 연결하는 간선(Edge)들의 집합으로 구성된 자료 구조이다.
- 정점(Vertex): 그래프의 구성요소로 하나의 연결점
- 간선(Edge): 두 정점을 연결하는 선
- 차수(Degree): 정점에 연결된 간선의 수
- 인접(Adjacency): 두 개의 정점에 간선이 존재(연결됨)하면 서로 인접해 있다고 한다.
- 경로(Path): 어떤 정점에서 시작하여 다른 정점으로 끝나는 순회로 두 정점 사이를 잇는 간선들을 나열한 것
- 싸이클(Cycle): 경로의 시작 정점과 끝 정점이 같음(시작한 정점에서 끝나는 경로)
V개의 정점을 가지는 무향 그래프는 최대 V * (V-1) / 2개의 간선이 가능하다.
선형 자료구조나 트리 자료구조로 표현하기 어려운 N:N관계를 가지는 원소들을 표현하기에 용이하다.
1. 그래프 유형
- 무향 그래프(Undirected Graph)

- 유향 그래프(Directed Graph)

- 가중치 그래프(Weighted Graph)
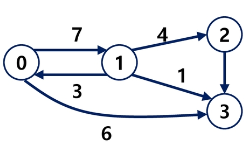
- 사이클 없는 방향 그래프(DAG, Directed Acyclic Graph)

- 완전 그래프
- 정점들에 대해 가능한 모든 간선들을 가진 그래프

- 부분 그래프
- 원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
- 트리도 그래프이다.
- 희소 그래프(Sparse Graph), 밀집 그래프(Dense Graph)
- 희소 그래프(Sparse Graph)는 간선이 얼마 없는 그래프이다.
- 밀집 그래프(Dense Graph)는 간선의 수가 최대 간선에 가까운 그래프이다.
2. 그래프 표현
간선의 정보를 저장하는 방식으로 메모리나 성능을 고려해서 결정한다.
- 인접 행렬(Adjacent matrix)
- V x V 크기의 2차원 배열을 이용해서 간선 정보를 저장
- 배열의 배열
- 정점 중심
- 인접 리스트(Adjacent List)
- 각 정점마다 다른 정점으로 나가는 간선의 정보를 저장
- 정점 중심
- 간선 리스트(Edge List)
- 간선(시작 정점, 끝 정점)의 정보를 객체로 표현하여 리스트에 저장
- 간선 중심
2-1. 인접 행렬(Adjacent matrix)
V x V 정방 행렬로 간선의 연결 유무를 배열에 저장하는 방식
adj[i][j]는 i에서 j로 가는 간선 정보를 의미한다.
두 정점이 인접되어 있으면 1, 그렇지 않으면 0으로 표현한다. (단, 가중치가 있다면 1이 아닌 해당 가중치로 표현한다.)
정점 대비 간선 수가 적은 그래프에서는 공간 효율성이 떨어진다.
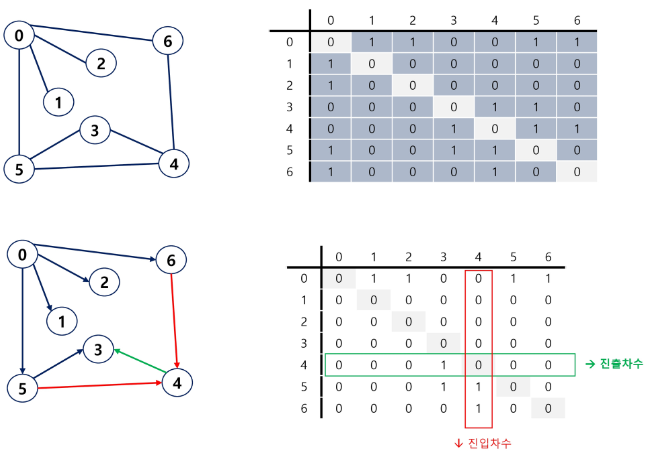
- 무향 그래프
- i번째 행의 합 = i번째 열의 합 = V_i의 차수
- 유향 그래프
- 행 i의 합 = V_i의 진출 차수
- 열 i의 합 = V_i의 진입 차수
- 인접 행렬의 단점
- 희소 그래프일 때, 공간 효율성이 떨어지고 탐색이 오래 걸린다.

구현
2-2. 인접 리스트(Adjacent List)
하나의 정점에 대한 인접 정점들을 각각 노드로 하는 리스트로 저장
LinkedList나 ArrayList를 활용해서 구현이 가능하다.
정점 대비 간선 수가 적을 때 공간 효율성에서 유리하다.

- 인접 리스트의 단점
- 밀집 그래프일 때, 링크따라 이동하는 만큼 탐색에 불리하다.
- 유향 그래프일 때, 나가는 정보만 보관하기 때문에 정점으로 들어오는 정보를 알기 어렵다.
- 이를 해결하기 위해 들어오는 정보를 보관하는 리스트를 하나 더 만들어야 한다.
구현
- LinkedList
- ArrayList
2-3. 간선 리스트
두 정점에 대한 간선 그 자체를 객체로 표현하여 배열로 저장

반응형