[알고리즘] 모든 쌍 최단 경로: 플로이드 워셜(Floyd-Warshall) 알고리즘

0. 최단 경로

최단 경로
간선의 가중치가 있는 그래프에서 두 정점 사이의 경로들 중에 간선의 가중치의 합이 최소인 경로

• 하나의 시작 정점에서 끝 정점까지의 최단 경로
  • 다익스트라(Dijkstra) 알고리즘
    • 음의 가중치를 허용하지 않음
  • 벨만-포드(Bellman-Ford) 알고리즘
    • 음의 가중치 허용
• 모든 정점들에 대한 최단 경로
  
  • 플로이드-워셜(Floyd-Warshall) 알고리즘

이번에는 이 중에서 플로이드-워셜(Floyd-Warshall) 알고리즘을 알아본다.

---

1. 플로이드-워셜(Floyd-Warshall) 알고리즘

모든 정점에서 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이다.

시작 정점에서 목표 정점의 최단 경로를 계산할 때, 다른 정점을 경유했을 때 비용을 비교하면서 구하는 방식이다.

DP 기법을 사용한 알고리즘으로 인접 리스트로 표현한다.

플로이드-워셜 알고리즘의 시간복잡도는 O(n^3)이며, 음의 가중치도 문제없이 사용이 가능하다.

음의 가중치가 없다는 가정 하에, 다익스트라보다 느리다.

1-1. 슈도 코드

D[start][end] //정점 start에서 정점 end로의 최소비용

For layOver in 1 -> n
    For start in 1 -> n (단, start ≠ layOver)
        For end in 1 -> n (단, end ≠ layOver, end ≠ start)
            D[start][end] <- min(D[start][layOver] + D[layOver][end], D[start][end])
        End For
    End For
End For

---

2. 수행 과정

위 그래프를 기준으로 알고리즘을 적용했을 때, 수행 과정을 스텝별로 살펴본다.

이 때, K는 경유지를 의미한다.

2-1. 경유지로 1번 노드를 지나갈 때

D[4, 2] = ∞에서 4 → 1 → 2 경로를 통하는 -2로 갱신

D[4, 3] = ∞에서 3 → 1 → 2 경로를 통하는 0으로 갱신

2-2. 경유지로 2번 노드를 지나갈 때

D[1, 5] = ∞에서 1 → 2 → 5 경로를 통하는 8로 갱신

D[5, 3] = 3에서 5 → 2 → 3 경로를 통하는 -2로 갱신

2-3. 경유지로 3번 노드를 지나갈 때

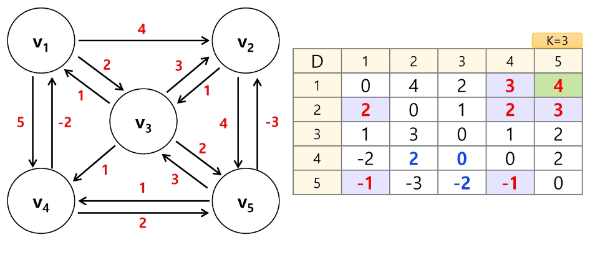
2-4. 경유지로 4번 노드를 지나갈 때

2-5. 경유지로 5번 노드를 지나갈 때

---

3. 구현

 3-1. 코드

3-2. 수행 과정 탐색용 코드

이 코드는 수행 과정에서 탐색했던 내용을 눈으로 확인하기 위해 작성된 코드이다.